fmap

Enables a gear which operates on a certain data type to be used with a complex data type that contains the type the gear knows how to handle.

fmap(din: Tuple, *, f, lvl=1, fcat=ccat, balance=None)

The Tuple fmap is useful in context where we need to operate on Tuple -s of some data types, and we already have gears that implement desired transformation but they operate on data types that are individual fields of the Tuple. The gears that process the Tuple fields are passed as a tuple (or any Python iterable) through the f parameter, and there should be as many gears as there are fields in the Tuple. If some of the fields should not be processed at all, None should be passed in their place for the f parameter.

Consider a simple example where a complex number is implemented as a Tuple, and we would like to multiply both the real and imaginary parts with a number 2. We don’t need to create a special gear for multiplying a complex number with a scalar, as we can reuse the mul() gear with a helm of the fmap():

drv(t=Tuple[Uint[16], Uint[16]], seq=[(0, 0), (1, 10), (2, 20)]) \
    | fmap(f=(mul(2), mul(2))) \
    | check(ref=[(0, 0), (2, 20), (4, 40)])

Under the hood, the fmap will be implemented as shown below: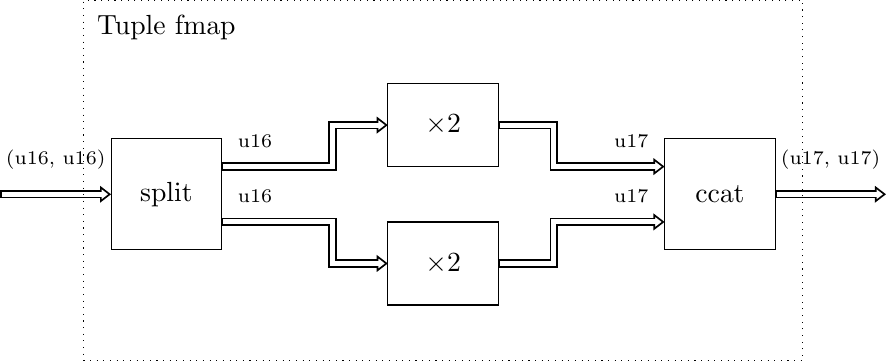

fmap(din: Union, *, f, fdemux=demux_ctrl, fmux=mux, balance=None)

The Union fmap operates ont the Union data types and enables to process the Union data values with different gears depending on the concrete type of the value. The gears that process the Union types are passed as a tuple (or any Python iterable) through the f parameter, and there should be as many gears as there are types in the Union. Unlike the Tuple fmap, only one of the gears is used to process the received value, i.e. only one gear is active at a time.

Following example processes the data that can either be signed or unsigned integers, and if value is signed it decrements it, otherwise nothing is done to the data:

drv(t=Union[Int[16], Uint[16]], seq=[(0, 1), (1, 1), (-10, 0), (-11, 0)]) \
    | fmap(f=(sub(b=1), None)) \
    | check(ref=[(0, 1), (1, 1), (-11, 0), (-12, 0)])

Under the hood, the fmap will be implemented as shown below: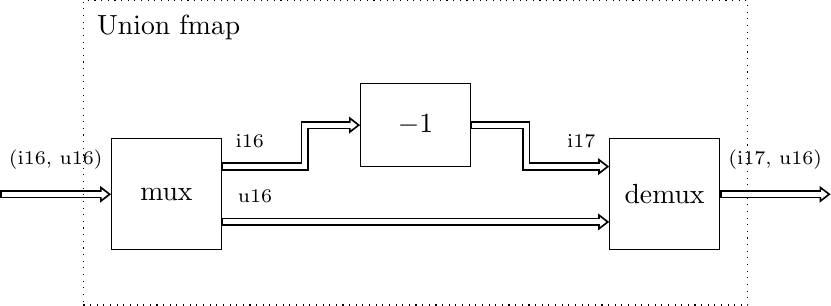

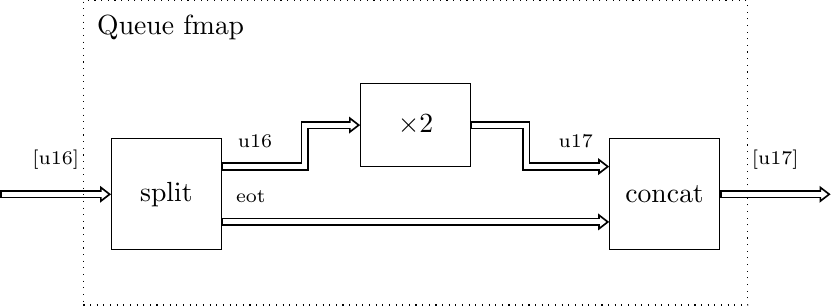
fmap(din: Union, *, f, lvl=1, fcat=czip, balance=None, common_balance=True)

The Queue fmaps are useful in context where we need to operate on Queue() -s of some data types, and we already have gears that implement desired transformation but operate on single data or lower level Queues.

Consider a simple example in which we want to multiply each element of a Queue with a number 2. We don’t need to create a special gear for this, as we can reuse the mul() gear with a helm of the fmap():

drv(t=Queue[Uint[16]], seq=[[0, 1, 2, 3, 4]]) \
    | fmap(f=mul(2)) \
    | check(ref=[[0, 2, 4, 6, 8]])

Under the hood, the fmap will be implemented as shown below: